REtipster does not provide tax, investment, or financial advice. Always seek the help of a licensed financial professional before taking action.
Whether you realize it or not, you are probably both a borrower and a lender, which means interest directly affects your finances.
You likely have a mortgage loan, perhaps many as a real estate investor. Plus a car loan, credit cards, perhaps student loans. And if you own bonds in your 401(k) or other retirement accounts, you have lent money through them as well.
But you may also earn interest on your savings account balance—money you’ve effectively lent your bank.
If you want to win the financial game in life, you need to understand its rules, and that means making interest work for you rather than against you.
What Is Interest?
When you lend someone money, you take on the risk that they won’t pay you back on time, or ever. You also lose the ability to invest that money elsewhere (like, say, in an income-producing rental property).
To compensate you for both your risk and your opportunity cost, you charge the borrower interest: a percentage of the loan balance that comes back to you as a return on your investment.
Related, but not identical, to the concept of interest is the annual percentage rate or APR. A loan’s APR includes the total interest charged, but also any fees or other costs associated with the loan. For example, if you borrow a hard money loan, the total cost of the loan includes not just interest but also points and lender junk fees. To calculate APR, you would add up the total interest charged plus all the fees, then divide them by the loan term.
Simple vs. Compound Interest
Lenders use two different models to calculate interest on a loan: simple and compound.
When lenders charge simple interest, they only charge based on the principal amount of the loan.
However, lenders using compound interest charge not just based on the loan principal but also any interest that has accrued. When borrowers start paying interest on their interest, their debts can quickly spiral out of control.
But for investors, the concept of compound interest can mean exponential growth on your returns. More on that later.
How to Calculate Simple Interest
As the name suggests, simple interest is easy enough to do on the back of a cocktail napkin. Perhaps even after it serviced a few cocktails.
The formula looks like this:
Simple Interest = P x (r x t)
The variables are:
- P: principal amount
- r: annual interest rate, as a decimal
- t: time or loan term, in years
If you borrow $100 at 3% interest for one year, you would calculate that by multiplying $100 x (.03 x 1) to reach a total interest amount of $3.
Examples of Simple Interest
To fully understand the different types of interest, it helps to see real-life examples.
Imagine you open a certificate of deposit (CD) paying 2% interest over a three-year term. If you put $1,000 in it, at the end of three years you’d get back your original $1,000 plus $60 in interest: $20 (2% of $1,000) for each of the three years. Put as an equation: $1,000 x (.02 x 3) = $60.
Alternatively, say you take out a $300,000 hard money loan charging 9% interest-only for one year. If you pay back the lender after exactly one year, you pay them $27,000 in interest: $300,000 x (.09 x 1) = $27,000.
But real life is messier, of course. Imagine instead that you pay them back after nine months. You instead pay them $20,250 in interest: $300,000 x (.09 x .75) = $20,250.
Amortization
Note that the calculation above assumes interest only, rather than amortizing the loan. When you borrow an installment loan such as a mortgage or car loan, they amortize it, so you pay both interest and principal with each monthly payment.
The formula for amortization is far more complicated:
Amortized Interest Payment = P x [r x (1+r)^n/([1+r]^n)-1]
Note that n represents the total number of payments or periods.
Unless you remember your high school math much better than I do, you won’t be doing that on a cocktail napkin after its intended use. Instead, just use a free loan amortization calculator online, like this:
How to Calculate Compound Interest
Unfortunately, compound interest is another complex calculation unsuited for cocktails.
The formula looks like this:
Compound Interest = P x [(1+r)^t – 1]
And that assumes annual compounding. The formula for other compound periods is even more complicated:
Compound Interest = P x [(1+[r/n])^n x t]
In this formula, n is the number of times interest is applied each time period, and t is the number of time periods elapsed.
Fortunately, you can skip the migraine headache and just use our compound interest calculator:
Examples of Compound Interest
A common example of compound interest is credit card balances. If you fail to pay off your balance in full each month, the card issuer charges you interest on your balance (the principal). Miss a payment on that, and the company charges you interest on not just your balance, but also the interest you owe.
As an easy comparison to simple interest, take the CD example above: 2% interest for a three-year loan. But imagine this time that it compounds annually. Instead of $60 in interest, it would pay out $61.21 in interest: $1,000 x [(1+.02)^3 – 1] = $61.21.
Not impressed with the $1.21 difference? Let’s up the ante to a 10% interest rate over a ten-year term, for a $100,000 investment. Simple interest would yield $100,000, while compound interest would yield $159,374.25: a difference of nearly $60,000.
Compounding: The Path to Riches or Ruin
As a borrower, you want to avoid compound interest like the plague. But as an investor, you want to put your money to work where it will compound and earn you returns on your returns.
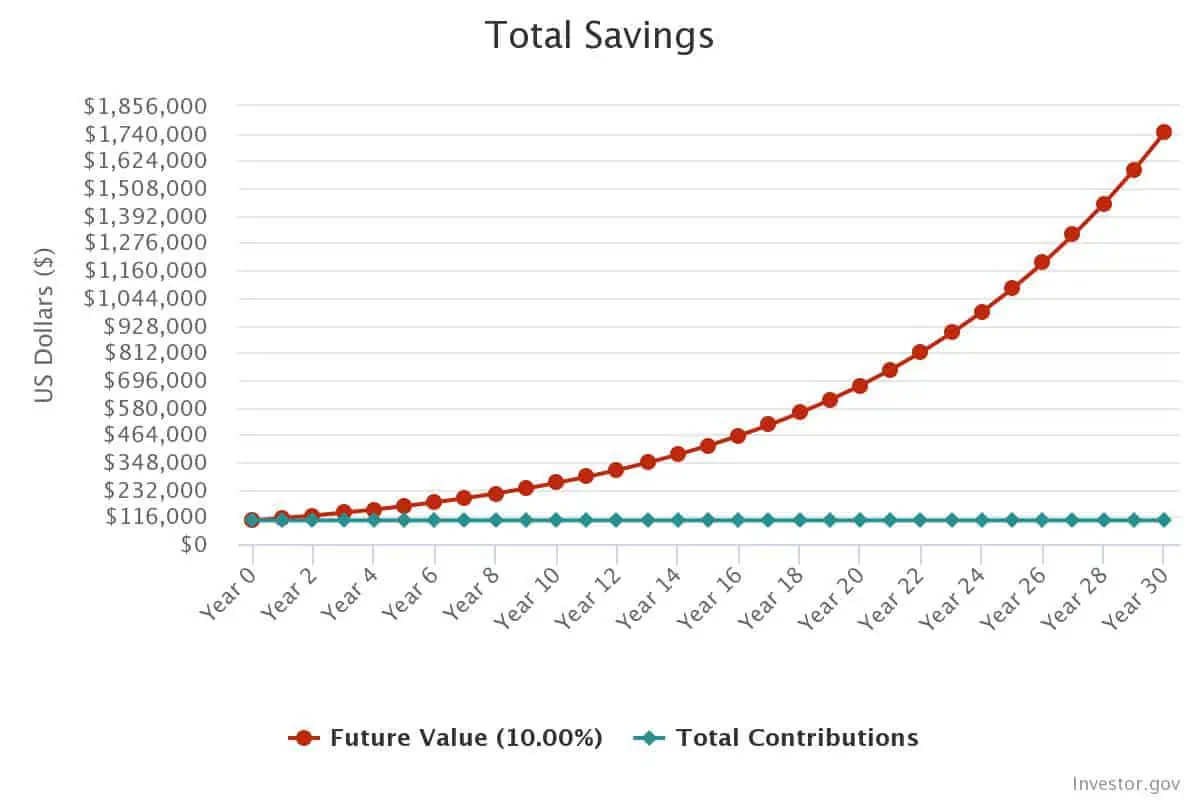
Consider a simple example. You invest $100,000 in a REIT that pays a 10% dividend yield, and select the option to reinvest dividends. After the first year, you have $110,000 in REIT shares. In the second year, your $110,000 in shares earns another 10% on itself, for an $11,000 gain. Your new balance in shares: $121,000. In the third year, you earn $12,100 in gains, for an ending balance of $133,100. In the fourth, you’d have earned $13,310 in returns, for a total of $146,410 in shares.
After ten years, you’d have earned $159,374.25 in returns, for a total balance of $259,274.25. After 20 years, you’d have earned $572,749.99 for a total of $672,749.99. By the end of 30 years, your total would reach $1,744,940.23—all from a one-time investment of $100,000.
In other words, compounding returns produce exponential growth. See for yourself:
The same logic applies no matter your investment. Stocks, rental properties, crowdfunding investments—as long as you reinvest your returns rather than pocket them, you earn returns on your returns.
The Power of Compounding in Real Estate
As a real estate investor, you have even more opportunities to put compounding returns to your advantage. You can participate in higher-yield investments such as syndications or private notes, to begin with. Higher returns steepen that exponential growth curve, letting you build wealth even faster.
But you can also use leverage to cover most of the cost of your investments with other people’s money. That can help improve your cash-on-cash returns and leave you with outsized passive income from little of your own money.
For instance, say you have $50,000. You use it as a down payment on a fixer-upper, renovate it, and sell it for a $50,000 profit after six months of ownership. Now you have $100,000, which you double again over the next six months. After one year, you’ve turned your $50,000 into $200,000. Just imagine the explosive growth curve on your money after three, five, or ten years!
Or instead, say you refinance the property and pull your original down payment back out, keeping the property as a rental rather than selling as a flip. You now have $300 in monthly cash flow from the rental, and you don’t have a single dime tied up in the property. So you turn around and do it again over the following six months. After the first year, you have $600/month in cash flow, or $7,200. As you add more cash flow, you can buy, renovate, rent, and refinance even more properties at any given time, accelerating your passive income indefinitely.
Final Thoughts
As you can see, compounding lies behind the surprisingly easy math behind retiring early with real estate. The more money you invest, the higher your rate of return, and the longer you leave the money to compound, the greater your results.
Of course, compounding cuts both ways. If you fall into debt and start paying interest on your interest, it can quickly bury you in a deep hole that you can’t easily escape from.
Focus on knocking out all unsecured debts, such as credit card balances and student loans, as quickly as you possibly can. Once free of them, start funneling as much money as you possibly can into high-return investments and reinvest the returns.
It sounds simple, and it is. But simple doesn’t always mean easy, as anyone who’s found themselves deep in debt knows.
What do you find confusing about simple versus compound interest?